std::next_permutation()
입력받은 원소의 다음 순열을 구함
다음 순열이 존재하면 true, 존재하지 않으면 false를 반환
$ {}_n \mathrm{P}_n $ 순열 출력
#include <iostream>
#include <algorithm>
#define N 4
int main(void) {
int arr[N] = { 1, 2, 3, 4 };
do {
for (int i = 0; i < N; i++) {
std::cout << arr[i] << " ";
}
std::cout << "\n";
} while (std::next_permutation(arr, arr + N));
return 0;
}
// output
// 1 2 3 4
// 1 2 4 3
// 1 3 2 4
// ...
// 4 3 1 2
// 4 3 2 1$ {}_n \mathrm{P}_r $ 순열 출력
#include <iostream>
#include <algorithm>
#define N 4
#define R 2
int main(void) {
int arr[N] = { 1, 2, 3, 4 };
do {
for (int i = 0; i < R; i++) {
std::cout << arr[i] << " ";
}
std::cout << "\n";
std::reverse(arr + R, arr + N);
} while (std::next_permutation(arr, arr + N));
return 0;
}
// output
// 1 2
// 1 3
// 1 4
// ...
// 4 2
// 4 3std::reverse() 함수를 사용하지 않고 결과를 출력하면 다음과 같이 같은 순열이 중복되어 출력된다.
// * WRONG *
// 1 2
// 1 2
// 1 3
// 1 3
// ...
// 4 2
// 4 2
// 4 3
// 4 3그 이유를 살펴보면, 우리는 앞에서부터 $ r $개의 원소만 필요한 데 반해 std::next_permutation() 함수는 모든 $ n $개의 원소의 순열을 구하기 때문이다. 예시로 든 $ n = 4 $, $ r = 2 $ 의 경우를 살펴보자. 밑의 코드 블럭에서 | 앞의 숫자들이 우리 눈에 보이는 결과물인데, 내부적으로는 4개의 원소를 전부 정렬하지만 출력은 앞에서부터 2개의 원소만 되기 때문에 마치 같은 순열이 중복된 것처럼 보인다.
// 1 2 | 3 4
// 1 2 | 4 3
// 1 3 | 2 4
// 1 3 | 4 2
// 1 4 | 2 3
// 1 4 | 3 2
// ...그렇다면 왜 std::reverse() 함수를 사용하면 문제를 해결할 수 있을까? $ n = 5 $, $ r = 2 $ 일 때 std::next_permutation()을 통해 다음과 같은 순열을 구한 상태를 가정하자.
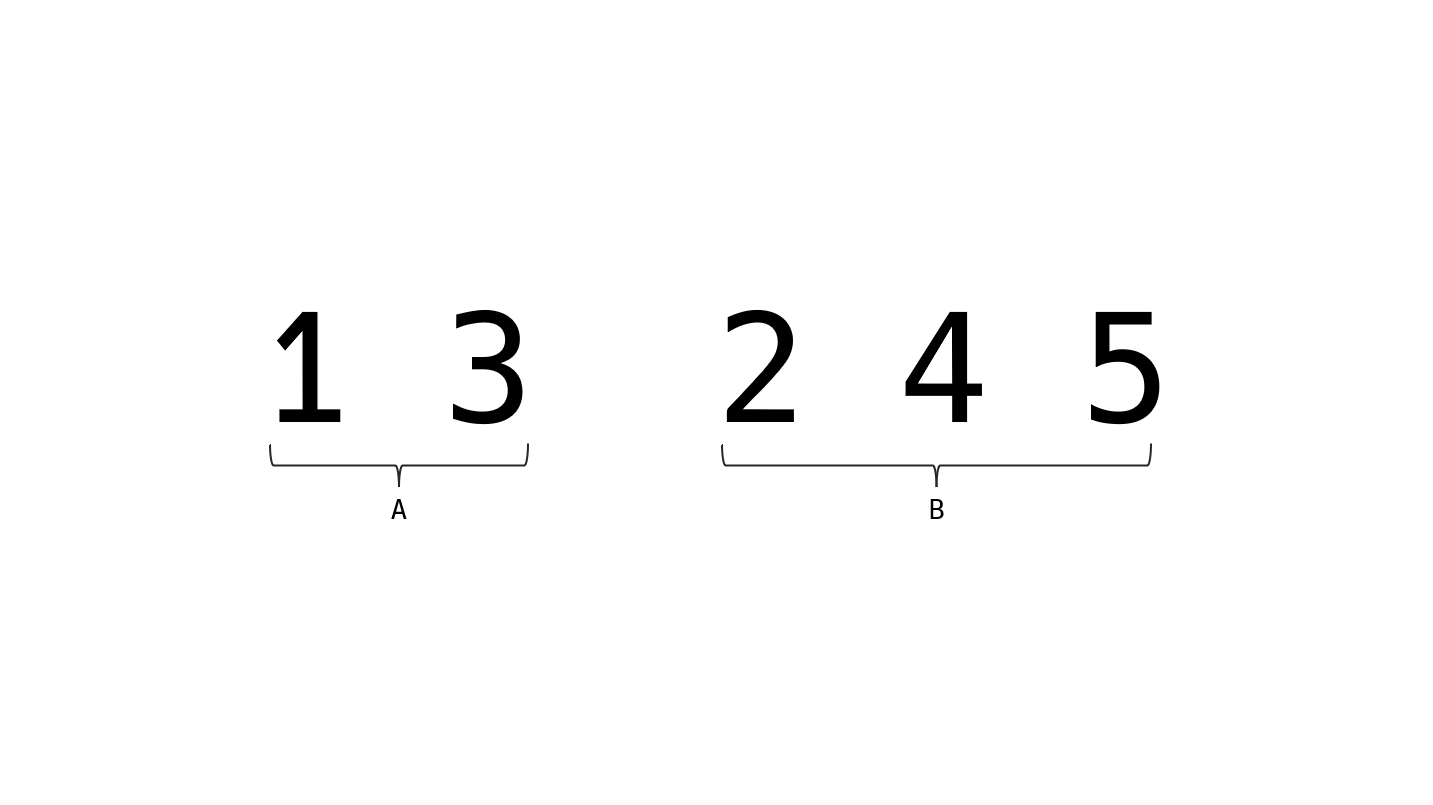
이 순열 중 우리가 필요한 $ 1 $번째 ~ $ r $번째 숫자들을 $ A $, $ r + 1$번째 ~ $ n $번째 숫자들을 $ B $ 라고 하자. 이때 $ B $로 이루어진 순열을 사전순으로 정렬하면 다음과 같다.

위 결과에서 $ B $의 첫번째 순열을 뒤집으면 제일 마지막 순열이 된다는 사실을 관찰할 수 있다. 즉
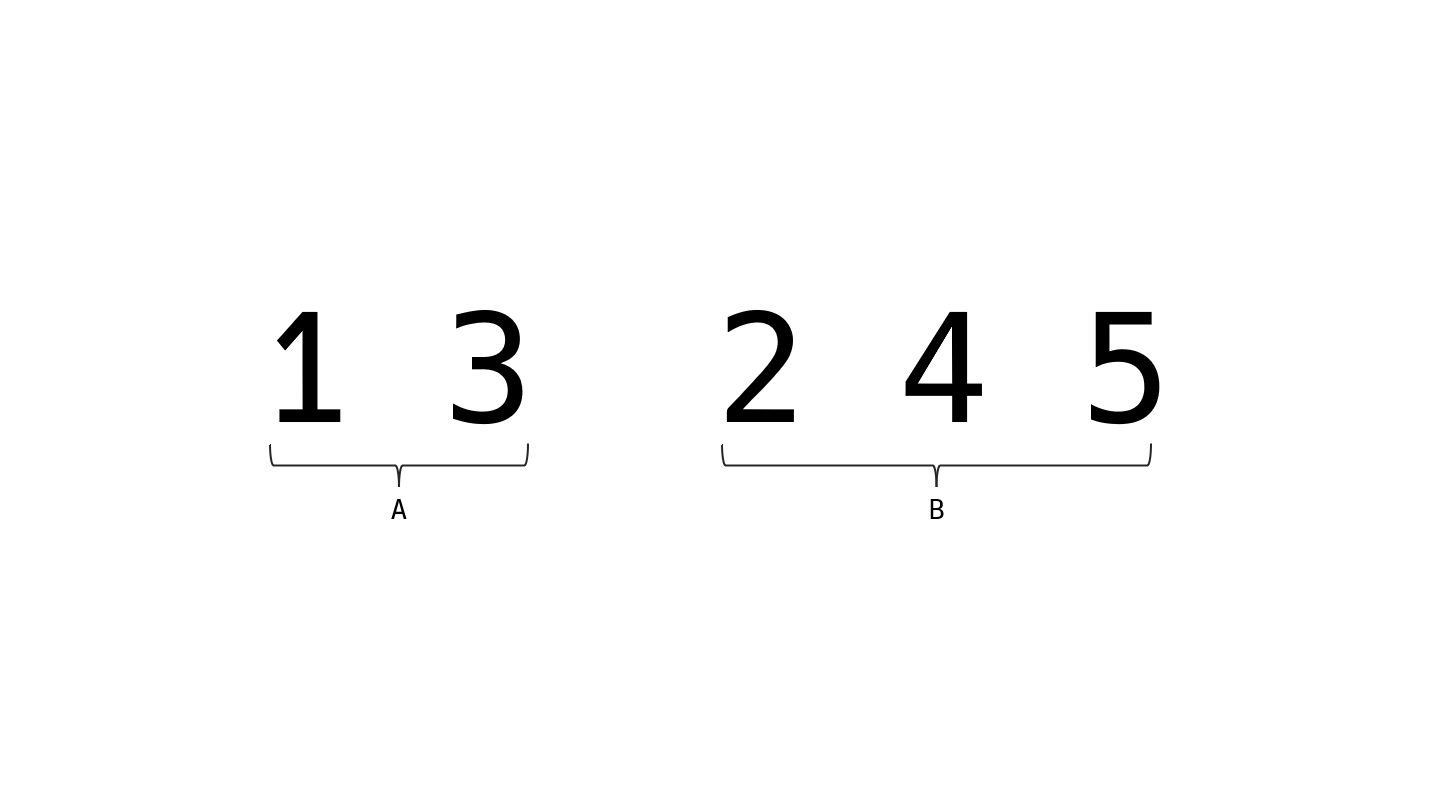
이 상태에서 $ B $를 뒤집고
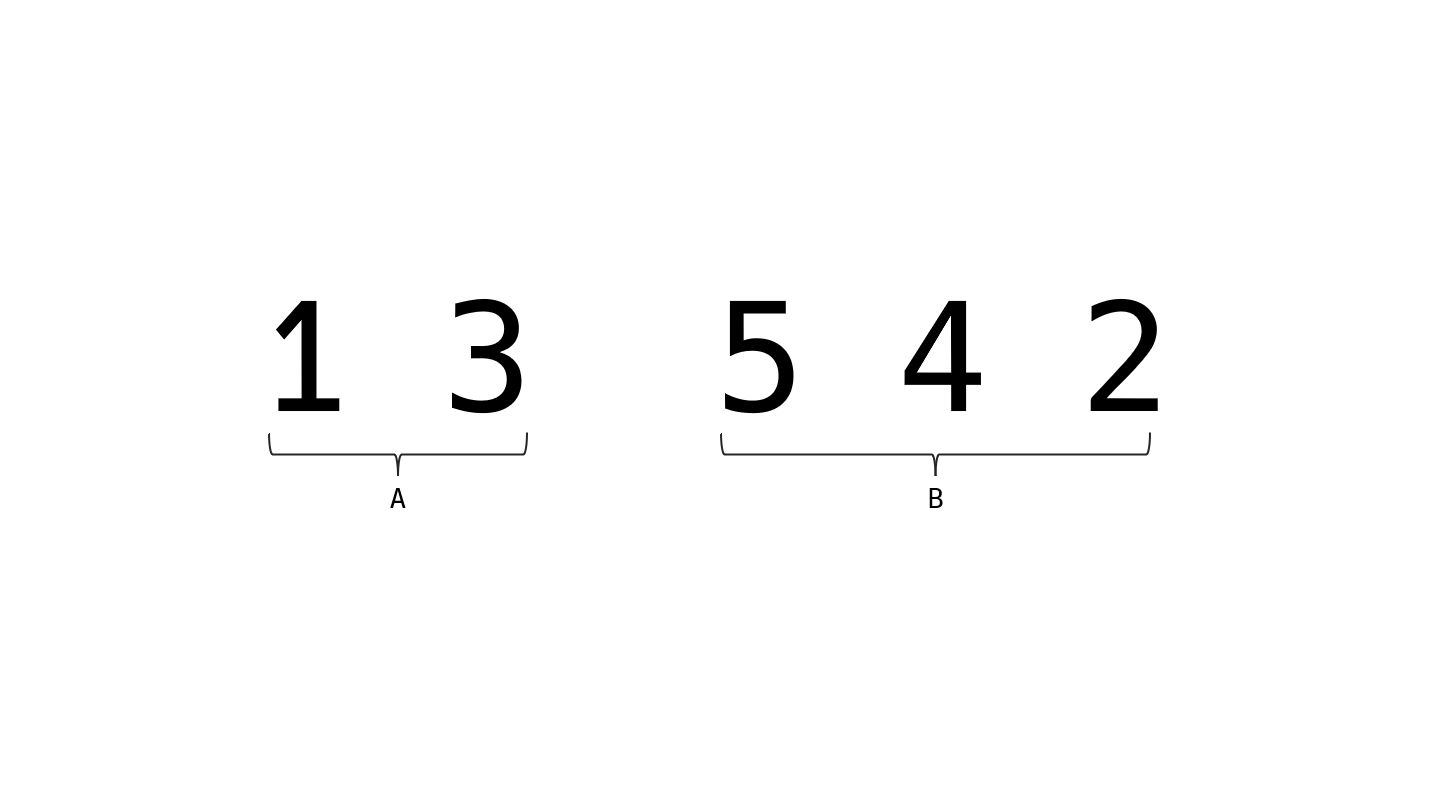
std::next_permutation() 함수를 실행하면
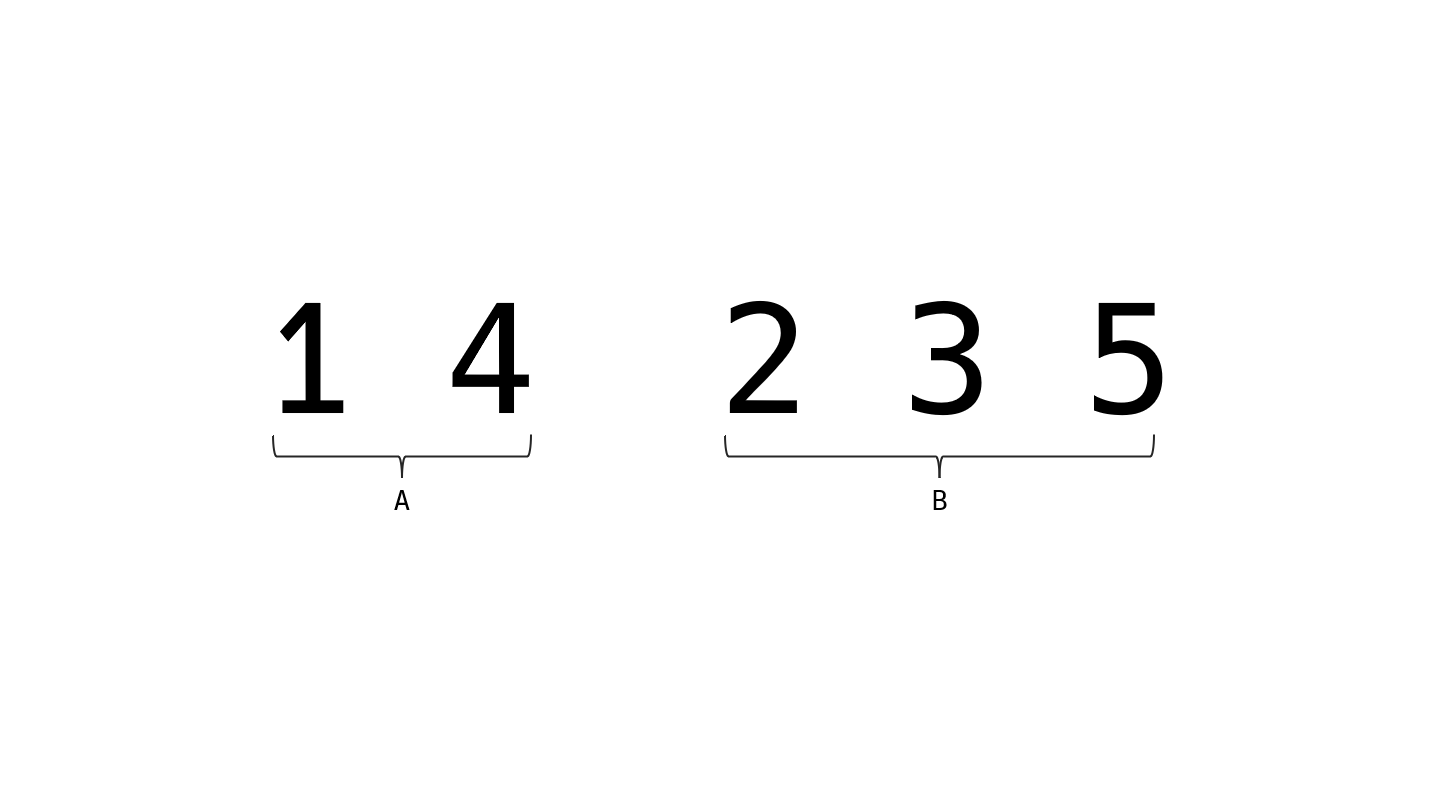
바로 우리가 필요한 다음 순열로 넘어갈 수 있다.
$ {}_n \mathrm{C}_r $ 조합 출력
#include <iostream>
#include <algorithm>
#define N 4
#define R 2
int main(void) {
int arr[N] = { 1, 2, 3, 4 };
int sel[N] = { 0, 0, 1, 1 };
do {
for (int i = 0; i < N; i++) {
if (sel[i] == 0) std::cout << arr[i] << " ";
}
std::cout << "\n";
} while (std::next_permutation(sel, sel + N));
return 0;
}
// output
// 1 2
// 1 3
// 1 4
// 2 3
// 2 4
// 3 4백트래킹 알고리즘을 통해 조합을 구할 때를 생각하면 된다. 주어진 데이터와 별개로 '선택 배열'을 하나 만들어서 데이터를 선택하는 모든 경우의 수를 구하면 된다. 주의할 점은 선택할 데이터를 $ 0 $, 선택하지 않을 데이터를 $ 1 $로 설정해야 한다. std::next_permutation() 함수는 오름차순으로 순열을 구하므로 선택할 데이터를 나타내는 값이 선택하지 않을 데이터의 값보다 크면 정상적으로 동작하지 않는다.
'C++' 카테고리의 다른 글
| 자주 사용하는 STL 정리 (0) | 2022.09.23 |
|---|
std::next_permutation()
입력받은 원소의 다음 순열을 구함
다음 순열이 존재하면 true, 존재하지 않으면 false를 반환
$ {}_n \mathrm{P}_n $ 순열 출력
#include <iostream>
#include <algorithm>
#define N 4
int main(void) {
int arr[N] = { 1, 2, 3, 4 };
do {
for (int i = 0; i < N; i++) {
std::cout << arr[i] << " ";
}
std::cout << "\n";
} while (std::next_permutation(arr, arr + N));
return 0;
}
// output
// 1 2 3 4
// 1 2 4 3
// 1 3 2 4
// ...
// 4 3 1 2
// 4 3 2 1$ {}_n \mathrm{P}_r $ 순열 출력
#include <iostream>
#include <algorithm>
#define N 4
#define R 2
int main(void) {
int arr[N] = { 1, 2, 3, 4 };
do {
for (int i = 0; i < R; i++) {
std::cout << arr[i] << " ";
}
std::cout << "\n";
std::reverse(arr + R, arr + N);
} while (std::next_permutation(arr, arr + N));
return 0;
}
// output
// 1 2
// 1 3
// 1 4
// ...
// 4 2
// 4 3std::reverse() 함수를 사용하지 않고 결과를 출력하면 다음과 같이 같은 순열이 중복되어 출력된다.
// * WRONG *
// 1 2
// 1 2
// 1 3
// 1 3
// ...
// 4 2
// 4 2
// 4 3
// 4 3그 이유를 살펴보면, 우리는 앞에서부터 $ r $개의 원소만 필요한 데 반해 std::next_permutation() 함수는 모든 $ n $개의 원소의 순열을 구하기 때문이다. 예시로 든 $ n = 4 $, $ r = 2 $ 의 경우를 살펴보자. 밑의 코드 블럭에서 | 앞의 숫자들이 우리 눈에 보이는 결과물인데, 내부적으로는 4개의 원소를 전부 정렬하지만 출력은 앞에서부터 2개의 원소만 되기 때문에 마치 같은 순열이 중복된 것처럼 보인다.
// 1 2 | 3 4
// 1 2 | 4 3
// 1 3 | 2 4
// 1 3 | 4 2
// 1 4 | 2 3
// 1 4 | 3 2
// ...그렇다면 왜 std::reverse() 함수를 사용하면 문제를 해결할 수 있을까? $ n = 5 $, $ r = 2 $ 일 때 std::next_permutation()을 통해 다음과 같은 순열을 구한 상태를 가정하자.
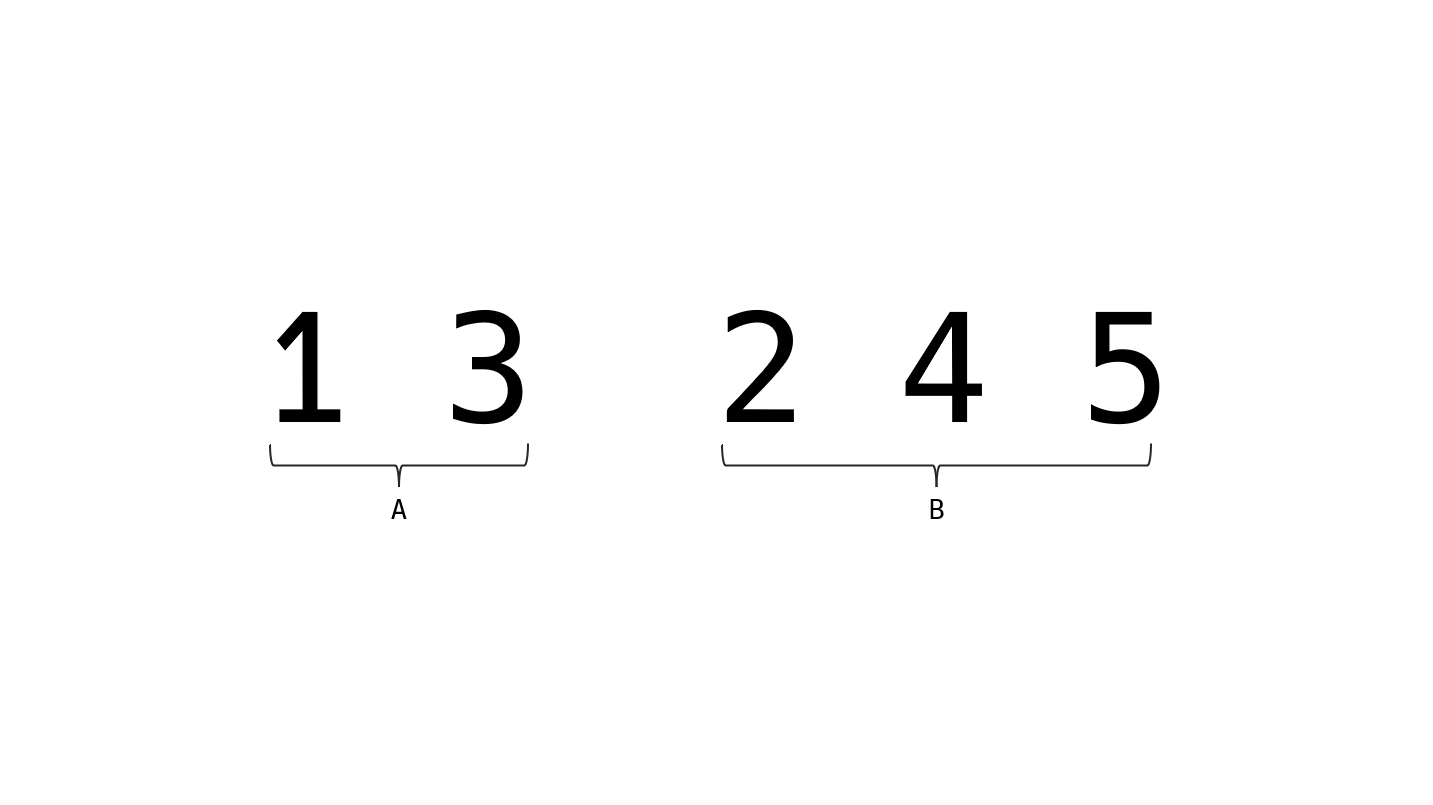
이 순열 중 우리가 필요한 $ 1 $번째 ~ $ r $번째 숫자들을 $ A $, $ r + 1$번째 ~ $ n $번째 숫자들을 $ B $ 라고 하자. 이때 $ B $로 이루어진 순열을 사전순으로 정렬하면 다음과 같다.

위 결과에서 $ B $의 첫번째 순열을 뒤집으면 제일 마지막 순열이 된다는 사실을 관찰할 수 있다. 즉
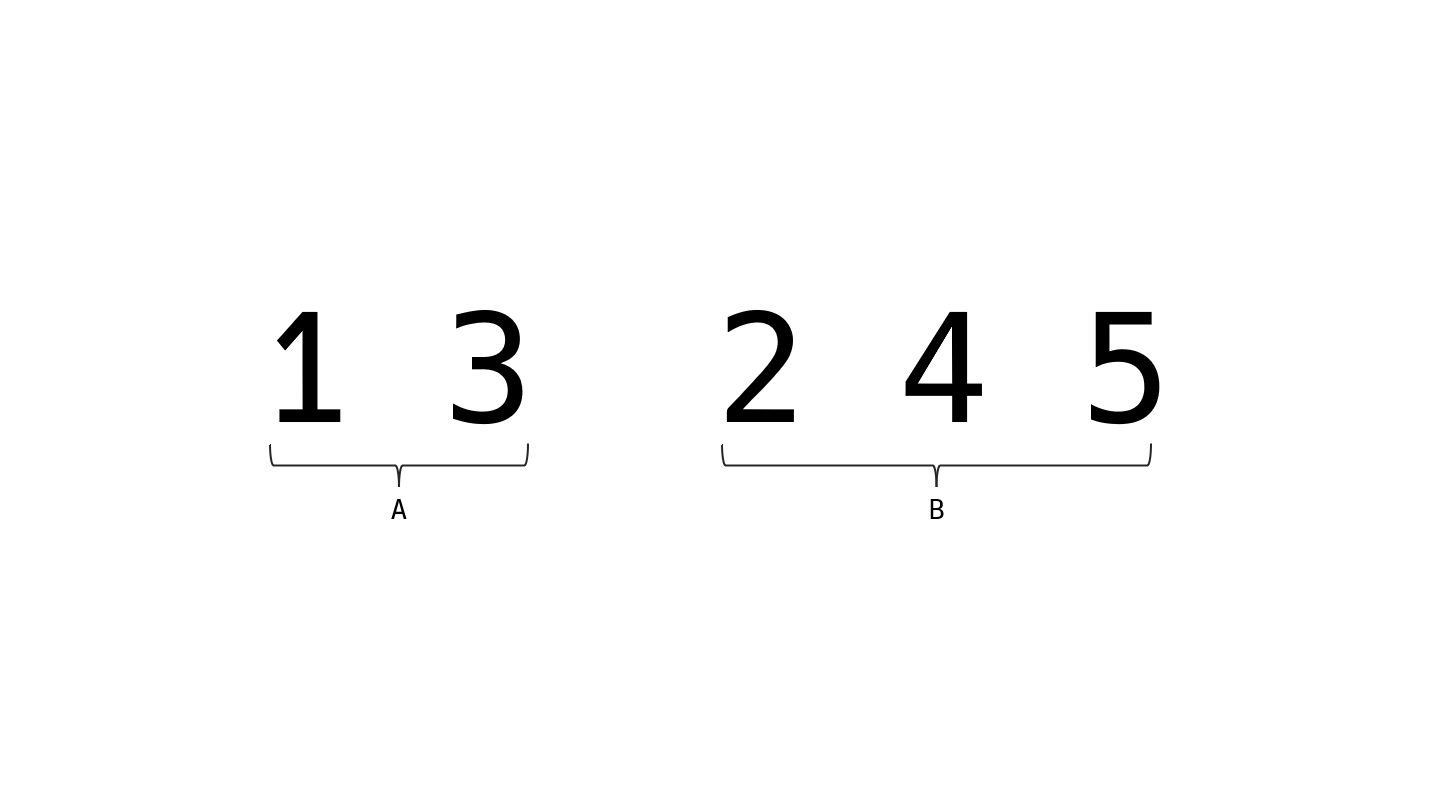
이 상태에서 $ B $를 뒤집고

std::next_permutation() 함수를 실행하면
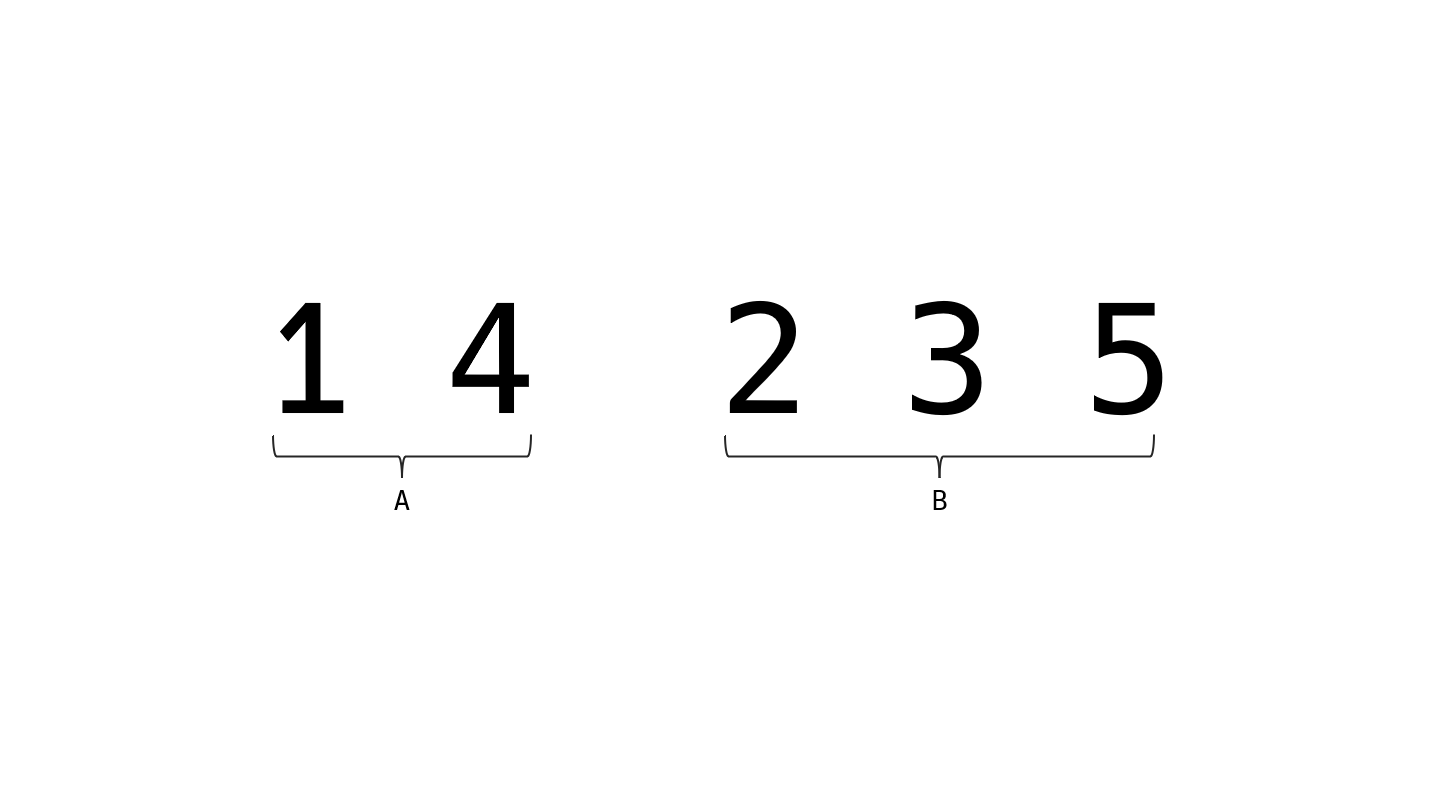
바로 우리가 필요한 다음 순열로 넘어갈 수 있다.
$ {}_n \mathrm{C}_r $ 조합 출력
#include <iostream>
#include <algorithm>
#define N 4
#define R 2
int main(void) {
int arr[N] = { 1, 2, 3, 4 };
int sel[N] = { 0, 0, 1, 1 };
do {
for (int i = 0; i < N; i++) {
if (sel[i] == 0) std::cout << arr[i] << " ";
}
std::cout << "\n";
} while (std::next_permutation(sel, sel + N));
return 0;
}
// output
// 1 2
// 1 3
// 1 4
// 2 3
// 2 4
// 3 4백트래킹 알고리즘을 통해 조합을 구할 때를 생각하면 된다. 주어진 데이터와 별개로 '선택 배열'을 하나 만들어서 데이터를 선택하는 모든 경우의 수를 구하면 된다. 주의할 점은 선택할 데이터를 $ 0 $, 선택하지 않을 데이터를 $ 1 $로 설정해야 한다. std::next_permutation() 함수는 오름차순으로 순열을 구하므로 선택할 데이터를 나타내는 값이 선택하지 않을 데이터의 값보다 크면 정상적으로 동작하지 않는다.
'C++' 카테고리의 다른 글
| 자주 사용하는 STL 정리 (0) | 2022.09.23 |
|---|
